Função do 2º grau- exercícios

- Raiz nada mais é do que os valores de x para qual a função vale zero!

O QUÊ??????????????

Calma, isso quer dizer que devemos calcular quais são os valores de x em que a parábola "corta" o eixo dos X.

Veja no exemplo abaixo o que é "raiz", graficamente:

Como já deve ter percebido, o exemplo tem DUAS raízes.

- E é sempre duas raízes?

Sim, uma função do segundo grau sempre terá DUAS raízes. Elas até podem ser iguais, mas sempre terá DUAS (se fosse do terceiro grau teria TRÊS, do quarto grau teria QUATRO...).

E para calcular as raízes desta função do segundo grau, utilizamos uma fórmula muito querida por todos que estudam no ensino médio (hehehe), a famosa fórmula de Bhaskara:

Onde cada letra desta fórmula representa os coeficientes da função do segundo grau que queremos resolver. Basta substituir e achar os valores. Podem notar que há um ± no meio da fórmula. Pois é, é daí que irá sair dois resultados: um com o sinal de + e outro com o sinal de -. Veja o exemplo:

Neste exemplo temos os coeficientes, a=2, b= -6 e c= -20   (Muita atenção para os sinais)
Agora substituindo na fórmula de Bhaskara:

Agora chegamos no momento crucial do cálculo das raízes.

Devemos separar esta conta em duas: uma com o sinal de + e a outra com o sinal de -. Assim:

Portanto as duas raízes da função 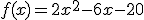 são 5 e -2.

Uma função para ser do 2º grau precisa assumir algumas características, pois ela deve ser dos reais para os reais, definida pela fórmula f(x) = ax² + bx + c, sendo que a, b e c são números reais com a diferente de zero. Concluímos que a condição para que uma função seja do 2º grau é que o valor de a, da forma geral, não pode ser igual a zero. 

Então, podemos dizer que a definição de função do 2º grau é: f: R→ R definida por f(x) = ax² + bx + c, com a Є R* e b e c Є R. 

Numa função do segundo grau, os valores de b e c podem ser iguais a zero, quando isso ocorrer, a equação do segundo grau será considerada incompleta. 

Veja alguns exemplos de Função do 2º grau: 

f(x) = 5x² – 2x + 8; a = 5, b = – 2 e c = 8 (Completa) 

f(x) = x² – 2x; a = 1, b = – 2 e c = 0 (Incompleta) 

f(x) = – x²; a = –1, b = 0 e c = 0 (Incompleta) 
Toda função do 2º grau também terá domínio, imagem e contradomínio. 

Exemplo 1 

A função do 2º grau f(x) = – x² + x – 2, pode ser representada por y = – x² + x – 2. Para acharmos o seu domínio e contradomínio, devemos primeiro estipular alguns valores para x. Vamos dizer que x = –3; –2; –1; 0; 1; 2. Para cada valor de x teremos um valor em y, veja: 

x = – 3 
y = – (–3)² + (–3) – 2 
y = –9 – 3 – 2 
y = – 12 – 2 
y = – 14 

x = – 2 
y = –( – 2)² + (– 2) – 2 
y = – 4 – 2 – 2 
y = – 8 

x = –1 
y = – (–1)² + (–1) – 2 
y = – 1 – 1 – 2 
y = – 2 – 2 
y = – 4 

x = 0 
y = 0² + 0 – 2 
y = – 2 

x = 1 
y = – 1² + 1 – 2 
y = – 1 + 1 – 2 
y = – 2 


x = 2 
y = – 2² + 2 – 2 
y = – 4 + 2 – 2 
y = – 4 

Exemplo 2 

Dada a função y = 2x² + x + 3, determine o conjunto imagem referente aos domínios –2, –1, 0, 1, 2, 3, 4. 

x = –2 
y = 2*(–2)² + (–2) + 3 
y = 2*4 – 2 + 3 
y = 8 – 2 + 3 
y = 9 

x = –1 
y = 2*(–1)² + (–1) + 3 
y = 2 – 1 + 3 
y = 4 

x = 0 
y = 2*0² + 0 + 3 
y = 3 

x = 1 
y = 2*1² + 1 + 3 
y = 2 + 1 + 3 
y = 6 

x = 2 
y = 2*2² + 2 + 3 
y = 8 + 2 + 3 
y = 13 

x = 3 
y = 2*3² + 3 + 3 
y = 18 + 3 + 3 
y = 24 

x = 4 
y = 2*4² + 4 + 3 
y = 32 + 4 + 3 
y = 39 

Exemplo 3 

Com relação à função f(x) = 3x² – 5x + m² – 9, sabe-se que f(0) = 0. Calcule o valor de m. 

f(0) = 0, isso significa que x = 0 e y = 0. A função f(x) = 3x² – 5x + m² – 9 pode ser escrita assim: y = 3x² – 5x + m² – 9, agora basta fazer as substituições: 

f(x) = 3x² – 5x + m² – 9 
f(0) = 3 * 0² – 5 * 0 + m² – 9 
0 = m² – 9 
m² = 9 
m = √9 
m = – 3 ou + 3

SINAIS DA FUNÇÃO DE 2º GRAU

MATEMÁTICA

Estudar o sinal de uma função, é determinar para quais valores reais de x a função é positiva, negativa ou nula. A melhor maneira de analisar o sinal de uma função é através do gráfico, pois permite-nos uma avaliação mais ampla da situação. Vamos analisar os gráficos das funções a seguir, de acordo com a sua lei de formação.                   Observação: para construirmos o gráfico de uma função do 2º grau precisamos determinar o número de raízes da função, e se a parábola possui concavidade voltada para cima ou para baixo.

∆ = 0, uma raiz real.
∆ > 0, duas raízes reais e distintas
∆ < 0, nenhuma raiz real.

Para determinar o valor de ∆ e os valores das raízes, utilize o método de Bháskara.

Coeficiente a > 0, parábola com a concavidade voltada para cima
Coeficiente a < 0, parábola com a concavidade voltada para baixo 

Exemplo 1

y = x² – 3x + 2
x² – 3x + 2 = 0

Aplicando Bháskara
∆ = (−3)² – 4 * 1 * 2
∆ = 9 – 8
∆ = 1



A parábola possui concavidade voltada para cima em virtude de a > 0 e duas raízes reais e distintas.

Análise do gráfico

 x < 1 ou x > 2, y > 0
 Valores entre 1 e 2, y < 0
 x = 1 e x = 2, y = 0


Exemplo 2

y = x² + 8x + 16
x² + 8x + 16 = 0

Aplicando Bháskara
∆ = 8² – 4 * 1 * 16
∆ = 64 – 64
∆ = 0

A parábola possui concavidade voltada para cima, em virtude de a > 0 e uma única raiz real.

Análise do gráfico

 x = –4, y = 0
 x ≠ –4, y > 0


Exemplo 3

y = 3x² – 2x + 1
3x² – 2x + 1 = 0

Aplicando Bháskara
∆ = (–2)² – 4 * 3 * 1
∆ = 4 – 12
∆ = – 8

A parábola possui concavidade voltada para cima em decorrência de a > 0, mas não possui raízes reais, pois ∆ < 0.

Análise do gráfico

 A função será positiva para qualquer valor real de x.

Exemplo 4

y = – 2x² – 5x + 3
– 2x² – 5x + 3 = 0

Aplicando Bháskara

∆ = (–5)² – 4 * (–2) * 3
∆ = 25 + 24
∆ = 49

A parábola possui concavidade voltada para baixo em face de a< 0 e duas raízes reais e distintas.

Análise do gráfico

 x < –3 ou x > 1/2, y < 0
 Valores entre – 3 e 1/2, y > 0
 x = –3 e x = 1/2, y = 0

Exemplo 5

y = –x² + 12x – 36
–x² + 12x – 36 = 0

Aplicando Bháskara
∆ = 12² – 4 * (–1) * (–36)
∆ = 144 – 144
∆ = 0

A parábola possui concavidade voltada para baixo em decorrência de a < 0 e uma única raiz real.

Análise do gráfico

 x = 6, y = 0
 x ≠ 6, y < 0

Vamos nos situar nos estudos. O que é vértice de uma parábola?
            - É o ponto em que a parábola atinge seu valor máximo ou mínimo.

Como assim?

Veja os exemplos abaixo:

O vértice de todas as parábolas tem uma característica própria, ele sempre se encontra "equidistante" de ambas as raízes, ou seja, a coordenada "x" do vértice fica exatamente no meio das coordenadas das duas raízes. Trocando em miúdos, a coordenada "x" do vértice é a média aritmética das coordenadas "x" das raízes, isto é, a soma das duas dividido por dois. Vamos chamá-lo de Xv ("x" do vértice):

Esta é a fórmula para encontrarmos o Xv. Se você não conseguir se lembrar na hora, faça a dedução como está aí em cima. É bem fácil!

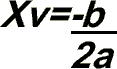Agora que já sabemos o Xv, devemos descobrir o Yv ("y" do vértice). Este valor podemos conseguir substituindo o "x" da função pelo "Xv", pois com isso estaremos calculando qual o valor de Y para o Xv, que é justamente o Yv ou f(Xv). A equação geral de uma função do segundo grau é f(x)=ax²+bx+c. Então vamos substituir todos "x" pelo valor de Xv da fórmula acima:

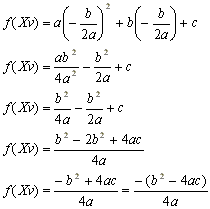
Veja que na última igualdade temos como denominador -(b²-4ac) e isso é justamente igual à -, portanto a fórmula final para o cálculo deYv, também chamado de f(Xv) é:

---

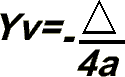IMAGEM

Agora que já vimos como calcular o Yv, podemos calcular a imagem de qualquer função do segundo grau.
Imagem, como vocês se lembram, é o conjunto de todos os valores do eixo Y em que a função existe.

O QUÊ ?????

Hehehe, já explico.

Imaginem agora uma prensa "esmagando" toda função em cima do eixo Y, como na animação abaixo:

A imagem da função será o conjunto de todos valores de Y que conseguirmos esmagar a função. No exemplo acima, o conjunto imagem é de 1 para cima, ou seja, é o intervalo [1, +∞).
Para calcular a imagem de qualquer função, temos que analisar somente duas coisas: a concavidade da parábola (sinal do coeficiente"a") e o valor do Yv.
Se o "a" for positivo (a>0) a concavidade é para cima, então a imagem é do Yv até "mais" infinito [Yv,+∞);
se o "a" for negativo (a<0) a concavidade é para baixo, então a imagem é de "menos" infinito até o Yv ∞,Yv]. Veja os exemplos abaixo:

f(x) = x2 - 15x +56	a>0 e portanto, o conjunto imagem desta função é o intervalo [-1/4,+∞)
f(x) = -2x2 + 12x - 16	a < 0 e portanto, o conjunto imagem desta função é o intervalo (-∞, +4]

Fazer uma análise de sinais em uma função quadrática pode ser muito útil para resolver inequações e também para determinar o domínio de algumas funções mais elaboradas (com divisão, com raiz quadrada...).

Vamos ver o que é a tal de "análise de sinal". Dê uma olhada na imagem abaixo:

Veja você que esta parábola (vendo da esquerda para direita) vem lá de cima (infinito) e vai descendo até o vértice, quando troca de sentido e passa a subir até o infinito novamente. Fazer a "análise de sinais" é verificar qual o sinal de Y em cada ponto do eixo X. Olhe novamente a figura. Até o ponto x=-3 a parábola está acima do eixo X, portanto ela é positiva. De -3 até 1 ela está abaixo do eixo X, portanto é negativa. Se houver um exercício, pedindo qual o intervalo em que esta parábola é negativa, a resposta será:

S = (-3, 1)

Note que foi utilizado parênteses, isso indica que o ponto -3 não está no intervalo, pois nele a função vale zero (está em cima do eixo). Idem para o ponto 1.

Exercícios

1) A representação cartesiana da função é a parábola abaixo. Tendo em vista esse gráfico, podemos afirmar que:

(A) a<0, b<0 e c>0 (B) a>0, b>0 e c<0 (C) a>0, b>0 e c>0 (D) a<0, b>0 e c<0 (E) a<0, b>0 e c>0

---

2) Qual a função que representa o gráfico seguinte?

(A) 
(B) 
(C) 
(D) 
(E) 

---

3) O valor mínimo do polinômio , cujo gráfico é mostrado na figura, é:

(A) 
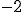
(B) 

(C) 

(D) 

(E) 

---

4) (UFRGS) As soluções reais da desigualdade 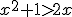 são os números x, tais que

(A) 
(B) 
(C) 
(D) 
(E) 

---

5) (UFRGS) O movimento de um projétil, lançado para cima verticalmente, é descrito pela equação . Onde y é a altura, em metros, atingida pelo projétil x segundos após o lançamento. A altura máxima atingida e o tempo que esse projétil permanece no ar corresponde, respectivamente, a

(A) 6,25 m, 5s
(B) 250 m, 0 s
(C) 250 m, 5s
(D) 250 m, 200 s
(E) 10.000 m , 5s

---

6) (UFRGS) Considere a função , definida por , com  e . O gráfico de f

(A) não intercepta o eixo das abscissas
(B) intercepta o eixo horizontal em dois pontos, de abscissas negativa e positiva respectivamente
(C) intercepta o eixo das abscissas em um único ponto
(D) intercepta o eixo das abscissas em dois pontos, ambos positivos.
(E) intercepta o eixo das ordenadas em dois pontos.

---

7) A razão entre a soma e o produto das raízes da equação 

(A) 

(B) 

(C) 

(D) 

(E) 

---

8) A solução de  é

(A) (0, 1)
(B) (-∞, 0)U(1, +∞)
(C) (-1, 1)
(D) (-∞, -1)U(1,+∞)
(E) R

---

9) (UFRGS) Para que a parábola da equação  contenha os pontos (-2; 1) e (3; 1), os valores de a e b são, respectivamente,

(A)  e 

(B)  e 

(C)  e 

(D)  e 

(E)  e 

---

10) O vértice da parábola que corresponde à função  é

(A) (-2, -2)
(B) (-2, 0)
(C) (-2, 2)
(D) (2, -2)
(E) (2, 2)

---

11) A figura abaixo ilustra uma ponte suspensa por estruturas metálicas em forma de arco de parábola.

Os pontos A, B, C, D e E estão no mesmo nível da estrada e a distância entre quaisquer dois consecutivos é 25m. Sabendo-se que os elementos de sustentação são todos perpendiculares ao plano da estrada e que a altura do elemento central CG é 20m, a altura de DH é:

(A) 17,5m
(B) 15,0m
(C) 12,5m
(D) 10,0m
(E) 7,5m

---

GABARITO
01-E	04-D	07-A	10-E
02-C	05-C	08-A	11 - B
03-C	06-B	09-B

Para ver a resolução destes exercícios, clique AQUI. Mas primeiro tente resolvê-los sozinho(a).